Apkrova įtemptiems lynams (lynų tilto apkrova)

Pagrindinės vertybės

Kabelių apkrovoms apskaičiuoti yra 5 pagrindinės vertės:

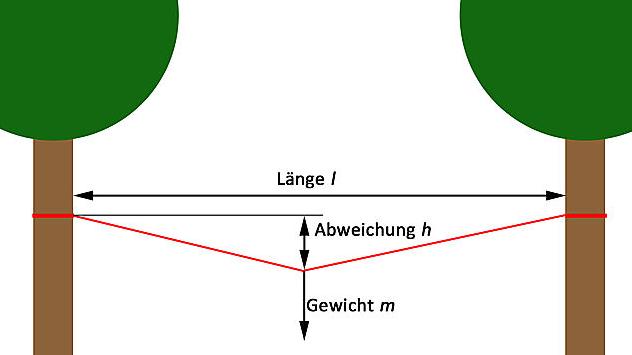
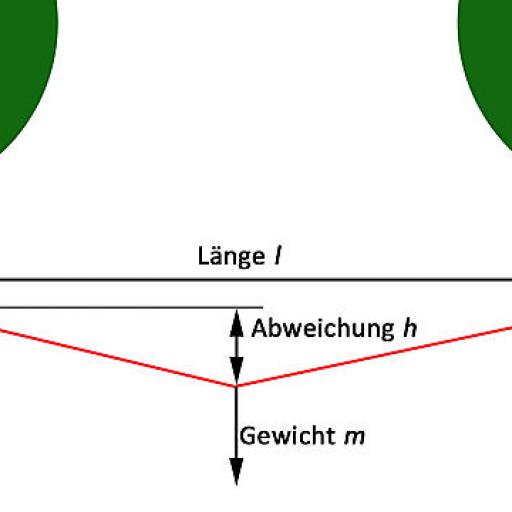
• Trosinio tiltoilgis l. Lynų tilto ilgis (ideali linija) metrais
• Svoris m ( masė), veikiantis įtemptą lyną
• Nuokrypis h Nuokrypis nuo idealios lyno linijos, veikiant masės m apkrovai
• Virvėstempimo stipris Rz. Ši vertė nurodoma N (Niutonais). Šiuolaikinių sintetinio pluošto lynų ši vertė gali būti didesnė nei 35 kN, tačiau senesnių lynų ji yra gerokai mažesnė. Paprastai ji turėtų būti bent 24 kN, kai naudojami lynų tiltai ir pan.
• Įtempimo jėga Fs, kuria įtempiamas lynas. Ši vertė paprastai būna nuo 3 iki 6 kN.

Skaičiuojant visada atsižvelgiama į apkrovą lyno centre, nes būtent tada lynas patiria didžiausią apkrovą.

Jėga niutonais

Svarbu žinoti jėgos vienetus: N (niutonas), daN (dekanevtonas), kN (kilonevtonas). Taikomi šie dydžiai:

1kN = 100daN = 1000N

Šie dydžiai dažnai maišomi su svorio dydžiais. Taikoma tokia tvarka:

Svorio jėga Fg [N] = masė m [kg] * sunkio jėgos pagreitis g [m/s2]

Kur g (sunkio jėgos pagreitis) yra konstanta 9,81 m/s2 (skaičiuojant mintinai: 10). Tai reiškia, kad jei ant virvės pakabinsite 1 kg masės, virvę veiks 9,81 N (1 kg * 9,81 m/s2 = 9,81 N).

Nepriežiūra

Apskaičiuojant lyno apkrovas, nepaisoma šių dalykų:

• Virvės savasis svoris

• Svorio apkrovos judėjimas (sūpynės judėjimas arba kritimai)

Kad kompensuotume šiuos dalykus ir dar turėtume atsargų, visada skaičiuojame su 1/3 lyno tempimo jėgos. Tai ypač svarbu virvėms, kurios naudojamos kaip paskutinė priemonė (saugos virvės).

Pagrindiniai principai

Taikomi šie 3 pagrindiniai principai:

• Kuo labiau virvė nusvirusi, tuo mažesnė apkrova
• Kuo ilgiau (didesniu atstumu) įtemptas lynas, tuo didesnė apkrova
• Kuo tvirčiau įtemptas lynas, tuo didesnė apkrova

Išvedimo ir (arba) apskaičiavimo metodas

Lyną veikianti apkrova apskaičiuojama taikant trigonometrinį ir vektorinį skaičiavimą. Jei neturite atitinkamų pagrindinių matematikos ar fizikos žinių, išvestinę sunku suprasti.

Šis skyrius skirtas tik užbaigti, žinoma, nesilaikoma nuomonės, kad jaunimo vadovas turėtų pats tai apskaičiuoti.

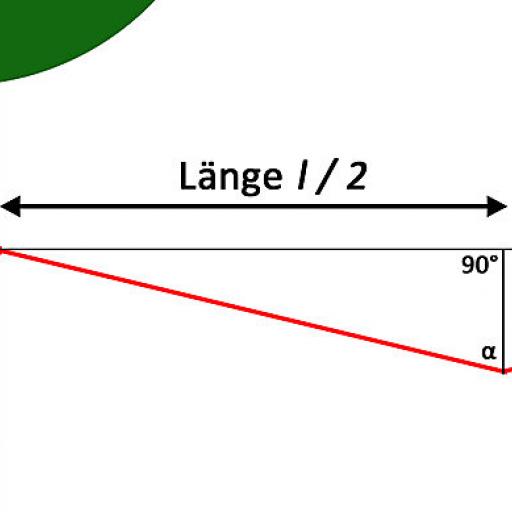
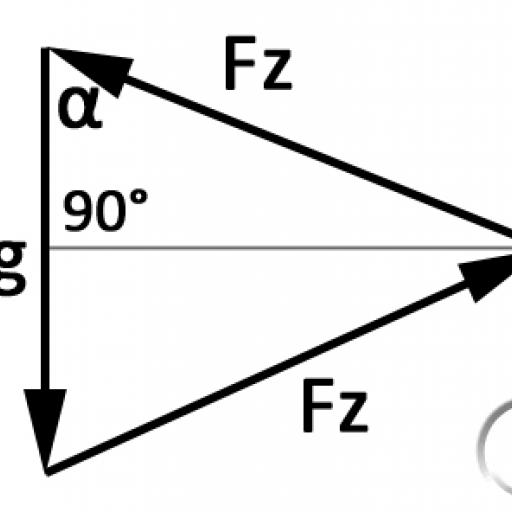
Pirmiausia reikia apibrėžti kampą α (1 pav.). Α taikoma tokia formulė: tan α = l/(2*h) iš to išplaukia: α = tan^-1(l/(2*h))

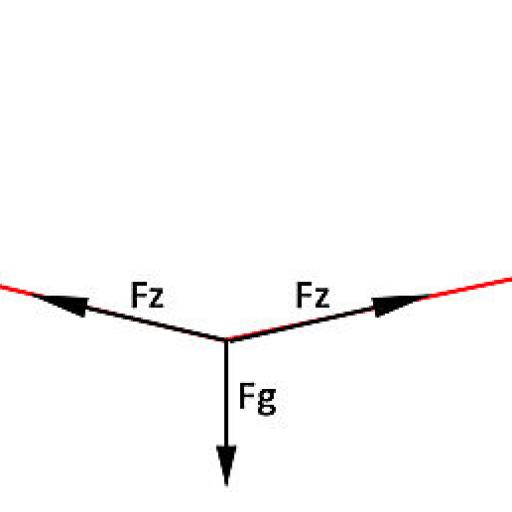
Trosą centre veikia trys jėgos: svorio jėga Fg ir dvigubai didesnė troso įtempimo jėga Fz (kiekviena skirtingomis kryptimis, žr. 2 pav.). Kadangi konstrukcija yra simetriška, Fz yra du kartus didesnė už tą pačią vertę. Kadangi visų tašką veikiančių jėgų vektorinė suma lygi 0, trys vektoriai sudaro trikampį(3 pav.)

Dabar šiame trikampyje Fz galima palyginti lengvai apskaičiuoti: įbrėžus trikampio aukštį, kampą α (kintamąjį kampą prieš tai apskaičiuotam kampui) ir pusę svorio jėgos, vėl galima sudaryti trigonometrinę lygtį: cos α = Fg/(Fz*2) iš to išplaukia: Fz = Fg/(cos α *2).

Jei dabar naudosite pirmiau pateiktos lygties reikšmę Alpha, pridėsite lyno įtempimo jėgą ir viską padauginsite iš 3, gausite galutinę reikiamą lyno tempimo jėgą (kuri išnaudojama tik 33 %):

Fo = (Fz + Fs)*3

Fo = (Fg/(cos α *2) + Fs)*3

Fo = (m*9,81/(cos(tan^-1(l/(2*h)))) *2) + Fs)*3

Šią lygtį galima transformuoti pagal poreikį, pvz:

m = (Fo/3 - Fs) * (cos(tan^-1(l/(2*h))) *2)/9.81

Pastaba: "Excel" formulė yra šiek tiek painesnė, nes "Excel" išveda trigonometrinių funkcijų rezultatus kaip radianus, kuriuos pirmiausia reikia perskaičiuoti.

Šaltinio nuoroda

• Viršelio paveikslėlis, "Excel" failas, nuotraukos, skaičiavimai: Pateikė Jungschar Schinznach / Manuel Meier