Belastung von gespannten Seilen (Seilbrückenbelastung)

Grundgrössen

Zur Berechnung von Seilbelastungen gibt es 5 Grundwerte:

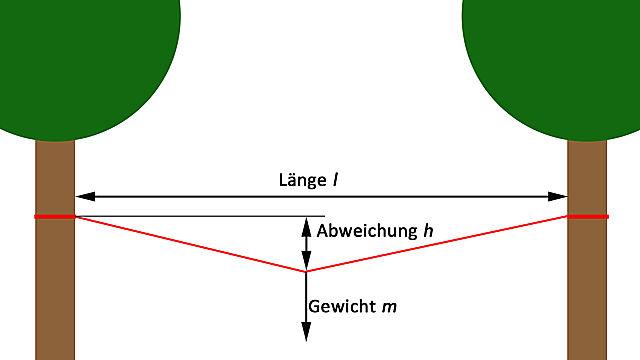
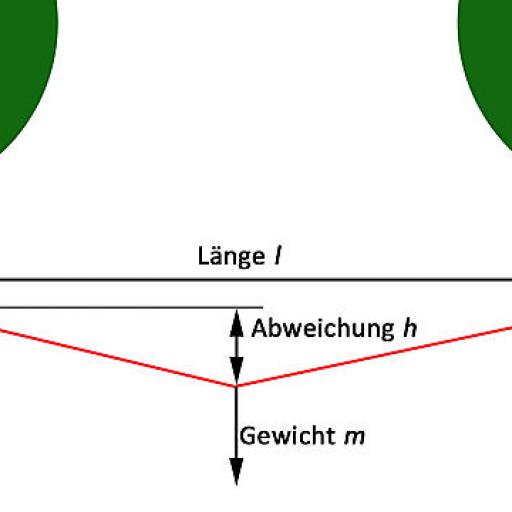
• Länge l der Seilbrücke. Die Länge der Seilbrücke (Ideallinie) in Metern
• Gewicht m (für Masse) die auf ein gespanntes Seil wirkt
• Abweichung h Abweichung von der Ideallinie des Seils, unter Belastung von Gewicht m
• Reissfestigkeit Rz des Seils. Angegeben ist diese Grösse in N (Newton). Bei modernen Kunstfaserseilen kann dieser Wert bei über 35kN liegen, bei älteren seilen jedoch deutlich tiefer, grundsätzlich gilt, dass sie für Seilbrücken u.ä. min. 24kN betragen sollte.
• Spannkraft Fs mit der ein Seil angezogen ist. Dieser Wert liegt i.d.R. zwischen 3 und 6kN.

Gerechnet wird immer mit der Belastung an der Mitte des Seils, da dann das Seil am stärksten belastet ist.

Kraft in Newton

Wichtig ist es, die Einheit für Kraft, N (Newton),  daN (Dekanewton), kN (Kilonewton) zu kennen. Es gilt:

1kN = 100daN = 1000N

Oft werden diese Angaben mit Gewichtsangaben gemischt. Dabei gilt:

Gewichtskraft Fg [N] = Masse m [kg] * Erdbeschleunigung g [m/s2]

Wobei g (Erdbeschleunigung) konstant 9,81m/s2 (zum Kopfrechnen: 10) beträgt. Das heisst, dass wenn man 1kg Masse an einem Seil aufhängt, 9,81N auf das Seil wirken (1kg * 9,81m/s2 = 9,81N).

Vernachlässigungen

Bei der Berechnung von Seilbelastungen werden folgende Punkte vernachlässigt:

• Eigengewicht des Seiles

• Bewegung der Gewichtslast (Schaukelbewegung oder Stürze)

Um diese Punkte zu kompensieren und auch noch Reserven zu haben, rechnen wir immer mit 1/3 der Reissfestigkeit des Seils. Vor allem für Seile, die als letzte sichernde Instanz gelten (Sicherungsseil) ist dies sehr wichtig.

Grundsätze

Grundsätzlich gelten folgende 3 Ansätze:

• Je mehr ein Seil durchhängt, desto geringer ist die Belastung
• Je Länger (grössere Distanz) ein Seil gespannt wird, desto grösser wird die Belastung
• Je stärker ein Seil angespannt wird, desto grösser wird die Belastung

Herleitung / Rechenweg

Die Berechnung der Belastung des Seiles erfolgt durch eine trigonometrische und vektorielle Berechnung. Wenn man nicht über die entsprechenden mathematischen bzw. physikalischen Grundkenntnisse verfügt, ist die Herleitung schwer nachvollziehbar.

Dieser Abschnitt ist nur zur Vervollständigung, es ist natürlich nicht die Meinung, dass ein Jungscharleiter dies selbst so berechnen können müsste.

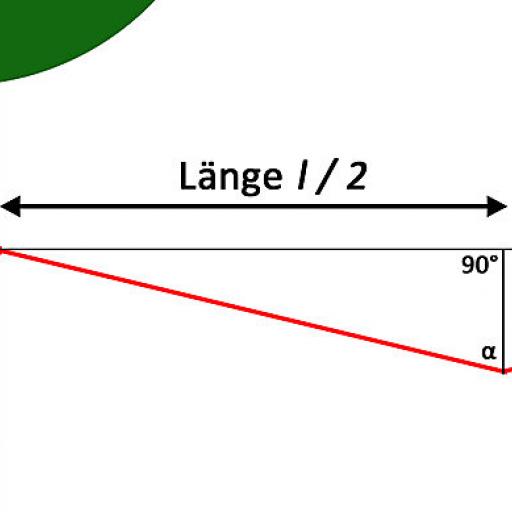
Als erstes muss Winkel α (Bild 1) definiert werden. Für α gilt: tan α = l/(2*h) daraus folgt: α = tan^-1(l/(2*h))

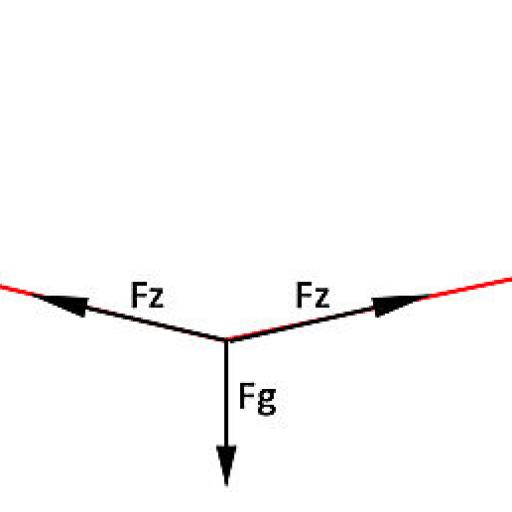
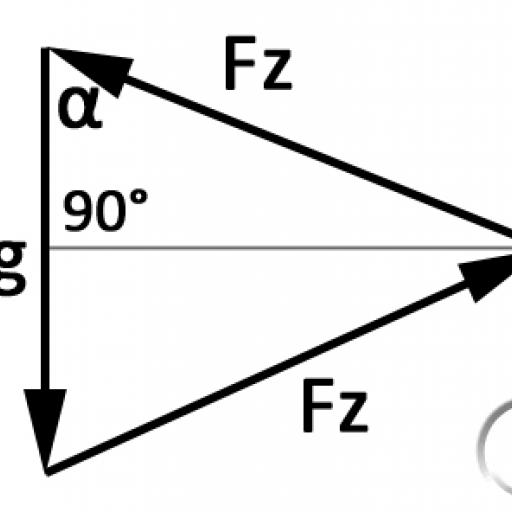
Auf den Mittelpunkt des Seils wirken 3 Kräfte: Die Gewichtskraft Fg, und zweimal die Seilzugkraft Fz (jeweils in unterschiedliche Richtungen, Siehe Bild 2). Da das Gebilde symmetrisch ist, ist Fz zweimal gleich gross. Da gilt, dass die vektorielle Summe aller Kräfte, die auf einen Punkt wirken 0 als Summe haben, bilden die drei Vektoren ein Dreieck (Bild 3)

In diesem Dreieck kann nun relativ einfach Fz berechnet werden: mit eingezeichneter Dreieckshöhe, dem Winkel  α (Wechselwinkel zum vorher berechneten Winkel) und der halben Gewichtskraft kann wiederum eine trigonometrische Gleichung aufgestellt werden:  cos α = Fg/(Fz*2) daraus folgt: Fz = Fg/(cos α *2).

Setzt man nun für Alpha den Wert der oberen Gleichung ein, addiert man die Spannkraft des Seils dazu und multipliziert man das ganze mit 3 kommt man auf die endgültig nötige Reissfestigkeit des Seils (die nur zu 33% ausgelastet wird):

Fo = (Fz + Fs)*3

Fo = (Fg/(cos α *2) + Fs)*3

Fo = (m*9,81/(cos(tan^-1(l/(2*h))) *2) + Fs)*3

Diese Gleichung kann nach Belieben umgeformt werden z.B.:

m = (Fo/3 - Fs) * (cos(tan^-1(l/(2*h))) *2)/9.81

Hinweis: Die Excel-Formel ist noch ein wenig verwirrlicher, da das Excel die Resultate von trigonometrischen Funktionen als Bogenmass ausgibt, dies muss zuerst zurückgerechnet werden.

Quellennachweis

• Titelbild, Excel-Datei, Bilder, Berechnungen: Zur Verfügung gestellt durch Jungschar Schinznach / Manuel Meier